REMEDIAL PAT MATEMATIKA WAJIB KELAS 10

Nama    : Camelia Zulfa (08)

Kelas     : X IPS 2

1. Nyatakan sudut 0,75 radian dan 0,35 radian ke dalam satuan derajat!

Pembahasan:

Sudut 0,35 dalam derajat adalah

= 0,35 • 360

= 126

Sudut 0,75 dalam derajat adalah

= 0,75 • 360

= 270

2. Nyatakan besar sudut berikut ke dalam satuan radian! 

a. 45° 15' 25"

Pembahasan:

45 : Pi ras = 180 derajat 

maka 45 derajat 

= 45/180 x Pi ras = 1/4 rad

• 15 : 15/180 x π

= 1/12 x π

= π/12

•25°:

= 25° 

= 25° rad

= 252 π rad

= 7π rad

b. 330° 23'

Pembahasan:

•25': 

= 25'

= 25: rad

= 252 π rad

= 7π rad

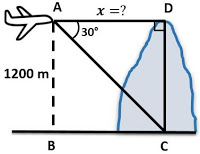
3. Seorang pilot pesawat melihat puncak gunung dari ketinggian 1200 m. Apabila sudut depresi (sudut lihat pilot terhadap arah mendatar) sebesar 30°, maka:

a. Gambarkan sketsa puncak gunung, posisi pesawat dan ketinggian dari tanah

Pembahasan:

AB adalah ketinggian dari tanah

AD adalah jarak pesawat ke puncak gunung

Sudut CAD adalah sudut depresi.

b. Tentukan jarak pesawat ke puncak gunung

Pembahasan:

tan = y/x

tan 30° = CD/AD

1/3√3 = 1200 m/x

x = 1200 m/1/3√3

x = 1200 m x 3/√3 x √3/√3

   = 1200 m x √3

   = 1200√3 cm

Nilai x = 1200√3 cm. 

Dengan demikian, jarak pesawat ke puncak gunung adalah 1200√3 cm.

4. Dua anak mengamati puncak pohon dari tempat yang bersebrangan seperti tampak pada gambat di bawah ini. Apabila anak pertama melihat dengan sudut elevasi 60° dan anak kedua dengan sudut elevasi 30° dan jarak kedua anak tersebut 200 m. Tentukan tinggi pohon tersebut!

Pembahasan:

AC = BC . COS 30° 

      = 200. 1/2 √3

      = 100 √3 m

AB= BC . COS 60° 

    = 200 . 1/2 

    = 100 m

t= AB . COS 30° 

 = 100 . 1/2 √3

 = 50 √3 m

Jadi tinggi pohon 50 √3 m

5. Sebuah tangga disandarkan pada suatu pohon kelapa yang batangnya lurus dan mempunyai buah siap panen. Sudut yang dibentuk oleh tangga itu dengan tanah (horizontal) adalah 60°. Jarak kaki tangga ke batang pohon kelapa hingga dapat meraih buah adalah 5 m, hitunglah jarak lintasan yang ditempuh seseorang untuk dapat mengambil buah pohon kelapa tersebut.

Pembahasan:

untuk mencari sisi miring : 

sin(60) = 5/x

x = 5/sin(60)

x = 5/√3/2 

x = 5 x 2/√3

x = 10√3/3 cm

6. Segitiga ABC siku-siku di C. Apabila sin A = 0.5, tentukan:

a. cos A dan tan A

Pembahasan:

Cos A = b/c = √3/2 = 1/2 √3

Tan A = a/b = 1/√3 = 1/3√3 

b. sec A dan cot A

Pembahasan:

Sec A = 1/Cos A = 1/ b/c = c/b = 2√3  = 2√3/3

Cot A = 1/Tan A = 1/ a/b = b/a = √3/1 = √3

7. Diketahui segitiga ABC siku-siku di B, jika panjang AC adalah 8 cm, dan siku-siku A = 30°. Hitunglah panjang AB dan BC.

Pembahasan:

Panjang AB DAN BC

  AB : AC = √3 : 2

  AB : 8    = √3 : 2

        2.AB = 8.√3

           AB =[8√3] /2

           AB = 4√3 cm

BC : AC    = 1 : 2

BC : 8       = 1 : 2

       2.BC  = 8 . 1

          BC  = 8/2

                 = 4 cm

8. Jika diketahui titik-titik koordinat sebagai berikut. Ubahlah menjadi koordinat cartesius dan koordinat kutub!

a. P (-6, 6√3)

Pembahasan:

P (-6 , 6√3) -> x negatif, y positif (kuadran 2)

r = √(x^2 + y^2)

r = √((-6)^2 + (6√3)^2)

r = √(36 + 108)

r = √144

r = 12

tan α = y/x

tan α = (6√3)/-6

tan α = -√3

α = 120°

Koordinat Kutub = (12 , 120°)

b. P (6√3, 60°)

Pembahasan:

P (6√3 , 60°)

r = 6√3

α = 60°

x = r . cos α = 6√3 . cos 60° = 6√3 . 1/2 = 3√3

y = r . sin α = 6√3 . sin 60° = 6√3 . 1/2√3 = 9

Koordinat Cartesius = (3√3 , 9)

9. Diketahui tan 25 = p, maka tentukan nilai dari tan 205° - tan 115° / tan 245° + tan 335°.

Pembahasan:

tan (180+25) - tan (90+25)

        -------------------------------------------

        tan (270-25) + tan (360°-25)

 = tan 25 + cot 25           p + 1/p

    ------------------------    =   -------------

    cot 25 - tan 25           1/p - p

= p²+1

   --------

      p

  ---------

    1-p²

  ---------

      p

= p²+1

   -------

   1-p²

=     p²+1

   ----------------

   (1+p) (1-p)

10. tan x = 1/2 maka nilai dari 2 sin x + sin (x + 1/2π) + cos (π - x) = ...

Pembahasan:

tan x = 1/2.

r^2=1^2+2^2

r^2 = 1 + 4

r^2 = 5

r = √5

sin x = 1/√5

COS X = 2/√5

2 sin x + sin (x + π/2) + cos (π-x)

= 2 sin x + (sin x cos π/2 + cos

x .sin.π/2) + (cos π cos x + sin π sin x)

= 2 sin x + ( sin x.0 + cos x .1) + (-1.cos x + = O.sin.x)

=2sin x + cos x - cos x

= 2 sin x

= 2(1/√5)

= 2/√5

= (2/5)√5.

11. Jika x di kuadran II tan tan x = a, maka tentukan nilai sin (90 + x)

Pembahasan:

12. Jika 54° = 1/x^1, maka cot 36° = ...

Pembahasan:

Tan 36/cot 54 = cot(90 - 36)

                        = cot 54.

cot54/cot54 = 1

13. cos 1200° = ...

Pembahasan:

cos (4 x 360 - 240)°

= cos 240°

= cos (270 - 30)°

= -sin 30°

= -1/2

14. sin 270 . cos 135 . tan 135 / sin 150 . cos 225 = ...

Pembahasan:

(sin 270 . cos 135 . tan 135) / (sin 150 . cos 225)

= ( (-1) . (-✓2 / 2) . 1) / (1/2 x . - ✓2/2)

=(✓2/2) / ✓2 / 4

=✓2 / x 4 / ✓2

=2

15. tan (-45°) + sin 120° + cos 225° - cos 30° = ...

Pembahasan:

tan (-45°) + sin 120° + cos 225°- cos 30°

= - tan 45° + sin 120° + cos 225° - cos 30°

= -1 + 1/2 √3 - 1/2 √2 - 1/2 √3

= -1 - 1/2 √2

16. Diketahui tan x = 2,4 dengan x berada di kuadran III. Nilai cos x adalah...

Pembahasan: 

Dik :

Tan x = 2,4

Kuadran III

Dit :

Cos x =....?

Jawab :

Tan x = 2,4 = 12/5

Tan = sisi depan/sisi miring

Sisi depan = 12

Sisi miring = 5

Cos = sisi samping/sisi miring

Sisi miring = √sisi depan ²+sisi samping²

=√12²+5²

=13

Karena di kuadran 3 hanya tan yang + maka cos dari 5/13 jadi -5/13

17. Diberikan segitiga sembarang ABC, seperti pada gambar di bawah ini! Tentukan panjang sisi AC!

Pembahasan: 

AC / sin C = AB / sin B

AC / 60° = 12 / 45°

AC / 1/2 √3 = 12 / 1/2 √2

AC / √3 = 12 / √2

AC = 12√3 / √2

AC = 12√6 / 2

AC = 6√6

18. Pada awalnya, Menara Pisa dibangun dengan ketinggian 56 m. Ternyata, tanah di lokasi pembangunan menara rentan akan kerapuhan, sehingga terjadi kemiringan. Pada jarak 44 m dari dasar menara diperoleh sudut elevasi 55°. Tentukan derajat kemiringan menara dari posisi awalnya!

Pembahasan:

Persoalan di atas bisa disederhanakan menjadi segitiga berikut.

Gunakan aturan sinus untuk menyelesaikan masalah di atas.

Dengan demikian, besar sudut A = 180° – (B + C) atau sudut A = 85°

Jadi, derajat kemiringan Menara Pisa adalah x = 90° – 85° = 5°

19. Jalan K dan jalan L berpotongan di kota A. Dinas tata kota ingin untuk menghubungkan Kota B dengan Kota C dengan membangun jalan M yang memotong kedua jalan yang ada (seperti gambar di bawah). Jalan antara Kota A dan Kota C adalah 5 km, dan sudut yang dibentuk oleh jalan M dan jalan  sebesar 75° sedangkan sudut yang dibentuk oleh jalan K dan jalan M adalah 30°. Tentukan jarak Kota A dan Kota B!

Pembahasan:

AB/sin C = AC/sin B

AB/sin 75° = 5/sin 30°

AB = 5.sin 75°/½

      = 5.2.sin 75°

      = 10.sin75°

      = 10.0,97

      = 9,7 km

20. Diberikan segitiga ABCD seperti pada gambar di samping. Luas ABCD adalah...

Pembahasan:

Panjang BD pada ABD

BD = √AB² + AD² = √12² + 5² = 13

menentukan luas segitiga ABD dan BDC

luas ABD = ½ x AB x AD

                  = ½ x 12 x 5 = 30 

luas BDC = ½ x DB x DC sin < BDC

                  = ½ x 13 x 10 x sin 60°

                  = ½ x 13 x 10 x ½ √3

                  = 65 / 2 x √3

menentukan luas ABCD

luas ABCD = luas ABD + luas BDC

                     = 30 + 65 / 2 √3

21. Pada sebuah segitiga ABC diketahui bahwa <A = 30° dan <B = 60°. Jika panjang sisi a + c = 9 cm, maka panjang sisi b adalah...

Pembahasan:

dik= <a = 30⁰

               <b = 60⁰

                a+c = 9cm

Dit= 6 =........?

 

JAWAB =

a + c = 9 cm

4 + 5 = 9 cm

b = √5² - 4²

   = √25 - 16

   = √9

b = 3cm

22. Diketahui segitiga ABC dengan panjang b = 3 cm, c = 3 cm dan <A = 60°. Maka tentukan panjang sisi a?

Pembahasan:

a² = b² + c² - 2bc cos a

     = 2² + 3² - 2.(2).(3) cos 60°

     = 4 + 9 - 12.⅓

     = 13 - 6

 a²= 7

  a = √7

23. Titik A dan C merupakan titik-titik ujung sebuah terowongan yang dilihat dari titik B dan besar sudut penglihatan < CBA = 60°. Jika panjang AB = 2x meter dan BC = 3x^2 meter, maka tentukan panjang terowongan?

Pembahasan:

24. Dua buah kapal tanker berangkat dari titik yang sama dengan arah berbeda sehingga membentuk sudut 60°. Kapal pertama bergerak dengan kecepatan 30 km/jam dan kapal kedua bergerak dengan kecepatan 25 km/jam. Tentukan jarak kedua kapal setelah berlayar selama 2 jam perjalanan?

Pembahasan:

Diketahui : 

sudut terbentuk = 60°

Kapal 1 = 30 km/jam

Kapal 2 = 25 km/jam

Jawab

AB 30 km/jam x 2 jam perjalanan = 60 km 

AC 25 km/jam x 2 jam perjalanan = 50 km

a2 = b2+c2 - 2bc cos a

      = 50(2) + 60(2) - 2 x 50 x 60 x cos 60

      = 2500 + 3600- 600 x 12

      = 4100 - 300

      = 3800

Jadi jarak antara dua kapal tersebut setelah berjalan 2 jam adalah 3800 km

25. Diberikan segitiga ABC dengan panjang AC = 6 cm, BC = 8 cm dan besar sudut C sebesar 30°. Luas segitiga ABC adalah...

Pembahasan:

luas = AC x BC x sin c/2

        = 6 x 8 x sin 30⁰/2

        = 24 x 1/2

        = 12 cm²

26. Sebuah kapal berlayar ke arah timur sejauh 30 km. Kemudian kapal melanjutkan perjalanan dengan arah 30° sejauh 60 km. Tentukan jarak terhadap posisi kapal berangkat?

Pembahasan:

<ABC = 90°+30°=120°

AC²=AB² + BC² - 2AB × BC cos <ABC

AC²=30² + 60² - 2 × 30 × 60cos 120°

AC2= 900 + 3600 +1800

AC²= √6300

AC²= √6300

=30√7 Mil

27. Diketahui segitiga ABC dengan panjang sisi AB = 9 cm, AC = 8 cm dan BC = 7 cm. Nilai sin A adalah...

Pembahasan:

BC² = AB² + AC² - 2 • AB • AC cos A

7² = 9² + 8² - 2 • 9 • 8 cos A

49 = 81 + 64 - 144cos A

49 = 145 - 144cos A

144cos A = 145 - 49

144cos A = 96

cos A = 96/144

cos A = ⅔

cos = samping/miring

samping = 2

miring = 3

maka : 

depan = √(miring² - samping²)

depan = √(3² - 2²)

depan = √(9 - 4)

depan = √5

sin A = depan/miring

sin A = (√5)/3

28. Diketahui segitiga ABC dengan < C = 30°. AC = 2a dan BC = 2a√3. Maka panjang AB adalah...

Pembahasan:

AB^2 = AC^2 + BC^2 - 2AC•BC•cosC

AB^2 = (2a)^2 + (2a akar3)^2 - 2(2a)(2a akar3)cos30°

AB^2 = 4a^2 + 12a^2 - 8a^2 akar3 (1/2 akar3)

AB^2 = 16a^2 - 12a^2

AB^2 = 4a^2

AB^2 = (2a)^2

AB = 2a

29. Sebuah segitiga ABC dengan panjang AB = 8 cm, BC = 13 cm dan AC = 15 cm. Jika x adalah sudut yang dibentuk antara sisi AB dan AC, maka nilai sin x . tan x = ...

Pembahasan:

BC^2 = AB^2 + AC^2 - 2.AB.AC.Cos x

13^2  = 8^2 + 15^2 - 2.8.15 cos x

169    = 64 + 225 - 240 cos x

240 coz x = 64 + 225 - 169

cos x = 120/240 =1/2

cos x = cos 60

x = 60°

sin x = sin 60° = 1/2 √3

cos x = cos 60° = 1/2

tan x = tan 60° = √3

30. Tentukan panjang sisi-sisi segitiga di samping!

Pembahasan:

PQ = √PR² + RQ²

       x + 1 = √(x - 1)² + (2√x + 2)²

       x + 1 = √x² - 2x + 1 + 4 (x + 2) 

       x + 1 = √x² - 2x + 1 + 4x + 8

       (x + 1)² = (√x² + 2x + 9)²

       x² + 2x + 1 = x² + 2x + 9

       x² - x² + 2x - 2x + 1 - 9 = 0

       0 = 0 > ∆ siku siku

       misal x = 2

       maka PR = x - 1 = 2 - 1 = 1 cm

                  RQ = 2√x + 2 = 2√2 + 2

                                          = 2√4 = 2 . 2 = 4

                  PQ = x + 1 = 2 + 1 = 3

31. Diberikan segitiga ABC dengan panjang AC = 6 cm, BC = 8 cm dan besar sudut C sebesar 30°. Luas segitiga ABC adalah...

Pembahasan:

L segitiga = 1/2 × AC × BC × sin 30

= 1/2 × 6 × 8 × 1/2

= 1/2 × 48 × 1/2

= 1/2 × 24

L segitiga = 12 cm²

32. Diketahui grafik fungsi y1 = 5 sin x dan y2 = sin 5x. Amplitudo y1 = ...

Pembahasan:

y1 = 1/2 (5-(5))

     = 1/2 (10)

33. Persamaan grafik fungsi trigonometri pada gambar di bawah ini adalah...

Pembahasan:

Amplitudo = ± 1

Pergeseran = 30° (kekanan)

Karena grafik awal merupakan minumum maka grafik CoS sehingga Amplitudo = -1, Persamaan -> y = -CoS (2x - 30°)

34. Gambarkan grafik fungsi y = tan x - 2, untuk 0  x ≤ 2 π = ...

Pembahasan:

35. Gambarkan grafik y = 2 sin 3 (x - 30°) untuk 0 ≤ x ≤ 180°.

Pembahasan:

36. Tentukan nilai maksimum dan minimum fungsi y = 3/2 cos(x+ ¼ π)+1

Pembahasan:

⅔cos(x+¼) = cos(x-¼)

36.⅔(cos x.cos  - sin x.sin¼) = cos x.cos¼- sin x.sin¼

⅔(cos x. 1/2 akar 2 - sin x. 1/2 akar

 ⅔) = cos x. ½akar2⅔+ sin x. 1/2 akar2

dibagi 1/2 akar ⅔

2cos x - 2sin x = cos x + sin x

cos x = 3 sin x

1/4= sin x / cos x

1/4 = tan x

37. Nilai maksimum dan nilai minimum dari fungsi y = 5 cos 3x adalah...

Pembahasan:

y = 3. cos 2x - 2

nilai maks terjadi saat cos 2x = 1 untuk x = 0°

y.maks = 3 . 1 - 2

= 3 - 2

= 1

nilai minimum terjadi saat cos 2x = - 1 untuk 2x = 180°

x = 90°

y.min = 3 (- 1) - 2

= - 3 - 2

= - 5

38. Periode dari fungsi y = 2 sin (3x - 30°) adalah...

Pembahasan:

2π/3

Penjelasan dengan langkah-langkah:

y = k cos (ax +b) periodenya adalah p = 2π/a

y = - 2 cos (3x +π/2) periodenya adalah p = 2π/3

39. Persamaan grafik di bawah ini adalah y = a cos kx, dengan 0° ≤ x ≤ 120°, maka nilai A dan K berturut-turut adalah...

Pembahasan:

y=cos kx

(0,2)—2=a.cos k(0°)

           2=a.cos 0°

              2=a

y=2.cos kx

(60°,-2) — -2=2.cos k.60°

cos k.60°=-1=cos 180°

k.60°=180°

k=3

40. Perhatikan grafik di bawah ini! Periode grafik fungsi di samping adalah...

Pembahasan:

2π/3 = 1/k . 2π →k = ±3

y = 2 . cos (3x)