LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

 Aturan Sinus dan Aturan Cosinus merupakan dua aturan yang menghubungkan panjang sisi dan besar sudut dalam segitiga sembarang dengan menggunakan konsep trigonometri. Sesuai dengan namanya, Aturan Sinus melibatkan fungsi sinus, sama halnya dengan Aturan Cosinus. Selain itu, luas segitiga ternyata dapat ditentukan dengan menggunakan bantuan trigonometri, yaitu didasarkan pada besar sudut dan panjang dua sisi yang mengapitnya.

Aturan Sinus

Aturan Sinus (Law of Sines atau Sines Law/Rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan.
Jika diberikan segitiga sembarang $ABC$ seperti gambar, maka berlaku persamaan berikut.
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$dengan $R$ adalah panjang jari-jari lingkaran luar segitiga $ABC$.

Aturan Cosinus

Aturan Cosinus (Law of Cosines atau Cosines Formula/Rule) adalah teorema yang digunakan untuk menentukan panjang sisi depan suatu sudut dengan menggunakan hubungan dua panjang sisi pengapit sudut tersebut dan nilai cosinusnya.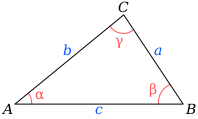

Pada segitiga $ABC$ di atas, berlaku
$$\begin{array}{cc}{a}^2& =b^2+c^2-2bc\cos \alpha \\ b^2& =a^2+c^2-2ac\cos \beta \\ c^2& =a^2+b^2-2ab\cos \gamma \end{array}$$

Aturan Luas Segitiga dalam Trigonometri

Misalkan $△ABC$ segitiga sembarang seperti gambar.

Dengan demikian, luas $△ABC$ dapat dihitung dengan rumus berikut apabila diketahui panjang dua sisi segitiga beserta besar sudut pengapitnya.
$\begin{array}{cc}{L}_{△ABC}& =\frac{1}{2}ab\sin C\\ & =\frac{1}{2}bc\sin A\\ & =\frac{1}{2}ac\sin B\end{array}$
Luas segitiga juga dapat dihitung bila diketahui panjang satu sisi dan besar tiga sudutnya.
$\begin{array}{cc}{L}_{△ABC}& =\frac{a^2\sin B\sin C}{2\sin A}\\ & =\frac{b^2\sin A\sin C}{2\sin B}\\ & =\frac{c^2\sin A\sin B}{2\sin C}\end{array}$

CONTOH SOAL

1. 

Pada $△JKL$, diketahui $\sin L=\frac{1}{3}$, $\sin J=\frac{3}{5}$, dan $JK=5$ cm. Panjang $KL$ adalah $\cdots \text{cm}$.
A. $5$                      C. $9$                      E. $15$
B. $7$                      D. $12$

Pembahasan:

Pada $△JKL$, sisi depan sudut $L$ adalah $JK$, sedangkan sisi depan sudut $J$ adalah $KL$. Dengan menggunakan Aturan Sinus, diperoleh
$$\begin{array}{cc}\frac{JK}{\sin L}& =\frac{KL}{\sin J}\\ \frac{5}{\frac{1}{3}}& =\frac{KL}{\frac{3}{5}}\\ 15& =\frac{KL}{\frac{3}{5}}\\ KL& =15\cdot \frac{3}{5}=9\end{array}$$Jadi, panjang $KL$ adalah $9\text{cm}$
(Jawaban C)

2. 

Jika dalam segitiga $ABC$ berlaku hubungan $a^2(1+\cos A)=2bc{\sin }^{2}A$, maka segitiga $ABC$ berbentuk $\cdots \cdot$
A. segitiga sama sisi
B. segitiga siku-siku
C. segitiga sama kaki
D. segitiga sembarang
E. segitiga tumpul

Pembahasan: 

Gunakan aturan cosinus bahwa $a^2=b^2+c^2-2bc\cos A$, serta identitas Pythagoras ${\sin }^{2}A=1-{\cos }^{2}A$.
Kita peroleh,
$$\begin{array}{cc}{a}^2(1+\cos A)& =2bc{\sin }^{2}A\\ (b^2+c^2-2bc\cos A)(1+\cos A)& =2bc(1-{\cos }^{2}A)\\ (b^2+c^2-2bc\cos A)(1+\cos A)& =2bc(1+\cos A)(1-\cos A)\\ b^2+c^2-2bc\cos A& =2bc-2bc\cos A\\ b^2-2bc+c^2& =0\\ (b-c{)}^2& =0\\ b& =c\end{array}$$Jadi, kita dapat simpulkan bahwa segitiga $ABC$ adalah segitiga sama kaki karena ada dua sisi yang panjangnya sama.
(Jawaban C)

3. 

Pada $△ABC$, diketahui bahwa $\angle B={70}^{\circ }$, $\angle C={80}^{\circ }$, dan $BC=2$ cm. Jika $R$ adalah panjang jari-jari lingkaran luar segitiga $ABC$, maka nilai $R=\cdots \text{cm}$.
A. $1$                     C. $4$                    E. $10$
B. $2$                     D. $8$

Pembahasan:

Menurut Aturan Sinus,
$$\frac{BC}{\sin \angle A}=\frac{AB}{\sin \angle C}=\frac{AC}{\sin \angle B}=2R$$dengan $R$ adalah panjang jari-jari lingkaran luar $△ABC$.
Karena $\angle B={70}^{\circ }$ dan $\angle C={80}^{\circ }$, maka $\angle A=(180-70-80{)}^{\circ }={30}^{\circ }$, sehingga
$$\begin{array}{cc}\frac{BC}{\sin \angle A}& =2R\\ \frac{2}{\sin {30}^{\circ }}& =2R\\ \frac{2}{\frac{1}{2}}& =2R\\ R& =2\end{array}$$Jadi, nilai $R=2\text{cm}$
(Jawaban B)